Désolé d'avoir un peu délaissé tout ça
Nous allons continuer avec l'utilisation des fractales en finance
Les mouvements des prix boursiers sont souvent considérés comme irrationnels, complètement aléatoires et chaotiques ( de simples changements peuvent avoir de grandes conséquences).
Le premier à avoir fourni des outils pour modéliser de telles variations est Louis Bachelier qui en 1900 a découvert ce que l'on a appelé par la suite le mouvement brownien. En quoi cela consiste-t-il ? Notons Z(t) un prix à un instant $t$. Le mouvement brownien stipule que Z(t+T) - Z(t) suit une loi normale de moyenne nulle et de variance proportionnelle à T; les lois normales indépendantes entre elles : c'est à dire que Z(t1+T) - Z(t1) suit une loi indépendante de Z(t2+T) - Z(t2). Le mouvement brownien ne sert pas uniquement pour modéliser les prix boursiers : on s'en sert aussi pour les mouvements des pétales de fleurs sur une solution aqueuse par exemple. Comme nous le verrons par la suite, le mouvement brownien semble inapproprié pour modéliser les mouvements des prix boursiers. Pour plus de précision, des outils mathématiques appelés fractales ont été développés.
Définition des fractales
La géométrie fractale a été créée par un mathématicien du nom de Benoit Mandelbrot.
Dans son livre, Mandelbrot définit les fractales de la façon suivante :
Les fractales sont des objets qu'on appelle irréguliers, rugueux, poreux ou fragmentés, et qui, de plus, possèdent ces propriétés au même degré à toutes les échelles. C'est dire que ces objets ont la même forme, qu'ils soient vus de près ou de loin.
Nous pouvons illustrer cette propriété par plusieurs exemples concrets : on retrouve la même structure sur un flocon de neige quelque soit l'échelle de précision avec laquelle on le regarde. Cela est également vraie pour la cote bretonne.
Concept d'auto-similarité
C'est la formalisation mathématique de la propriété que nous venons d'évoquer. Cela veut dire que chaque partie d'un objet peut être obtenue en transformant l'objet en entier par une similitude ( une similitude est une famille de transformations mathématiques qui comprend les réductions et les compressions linéaires).
On peut aussi étendre cette notion sur les distributions de probabilités.
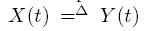
signifie que X et Y sont deux variables aléatoires qui ont la meme distribution.
On dit que les incréments d'une distribution X sont auto similaires lorsque il existe un H tel que :

Article fondateur de Mandelbrot
Mandelbrot a écrit son premier article sur le sujet en 1963 intitulé The variation of certain speculative prices. Mandelbrot va constater tout d'abord que le mouvement brownien ne convient pas pour plusieurs raisons. Premièrement, le coefficient kurtosis et le skewness données par la distribution des prix boursiers ne correspondent pas à ceux de la loi normale ( autrement dit les « cloches » sont plus pointues et moins plates que celle de la loi normale).
Les queues de la distributions sont beaucoup plus épaisses : les valeurs extrêmes sont prises beaucoup plus souvent. Le moment d'ordre 2 varie de façon erratique et ne converge pas quand la taille de l'échantillon devient très grande (alors que le moment d'ordre 2 d'une loi normale converge).Les courbes postulées par le mouvement brownien sont continues alors qu'il y a des discontinuités dans la réalité : en effet, il y a parfois de très brusques variations des prix boursiers (par exemple lors des krachs). Tous ces éléments vont faire que Mandelbrot va abandonner l'hypothèse de normalité et chercher d'autres types de distributions capables de mieux représenter les indices boursiers.
Les distributions L Stables
Les distributions L-Stables permettent d'avoir des distributions fractales. Nous les avions vus dans le premier billet. En effet, supposons que pour modéliser
Z(t+ to) - Z(t) les variations d'un prix boursier d'une semaine, on prenne une distribution L-Stable. Si on additionne quatre fois les variations successives d'une semaine, on obtient une variation sur un mois. Or par la propriété d'invariance par addition, la variation sur un mois est une distribution de la même forme que celle sur une semaine. Comme nous le verrons par la suite, les prix boursiers vérifient bel et bien cette propriété. La raison de cette invariance par l'échelle est inconnue pour le moment, c'est un fait observé.
Comportement asymptotique
Nous avons déjà dit que les queues des distributions des prix boursiers étaient plus épaisses que celles des lois normales. Nous allons donc nous intéresser au comportement asymptotique d'une distribution L-stable U. Levy a montré que toute loi L Stable non gaussienne va asymptotiquement suivre une loi de Pareto . C'est à dire que lorsque u tend vers l'infini, il existe deux constantes C1 et C2 telles que :

Pour modéliser le fait que changements de prix prennent souvent des valeurs extrêmes, supposons que les moments sont infinis au delà du premier. Cela revient pratiquement a prendre des lois de Pareto.
Si le moment d'ordre 1 converge : p(u)u tend vers 0. Et si le moment d'ordre 2 diverge : p(u) décroit moins vite que u²
Les expressions les plus simples pour arriver à cela sont les lois de Pareto
Dans le prochain billet, nous verrons les mouvements browniens fractionnaires et la mémoire longue.
Aucun commentaire:
Enregistrer un commentaire